テキストエディタのデータ構造
テキストエディタでよく使われるデータ構造には、Gap Buffer、Piece table、Rope を元にしたものが多いです。
テキストエディタでは、テキストファイルの任意の場所への挿入や削除が繰り返されます。 単純な文字列(ここでは文字配列)をデータ構造として利用した場合、編集の都度メモリのコピーが必要になります。
元のテキスト char[] text に、char[] ins の文字列配列を、index の位置に挿入する場合、以下のような処理となり、テキストが長い場合、メモリのコピー処理がボトルネックになります。
int index = 100; char[] ins = "insert text".toCharArray(); char[] dest = new char[text.length + ins.length]; System.arraycopy(text, 0, dest, 0, index); System.arraycopy(ins, 0, dest, index, ins.length); System.arraycopy(text, index, dest, index + ins.length, text.length - index);
都度メモリコピーが行われないようにするには、テキストを行単位に分割し、双方向リストで扱う方法が考えられます。ただし、双方向のポインタを保持するため、メモリ使用量が増加します。さらに、双方向リストなのでランダムアクセスに弱く、特定の要素を見つけるのにリストの先頭から順に辿る必要があるといった欠点があります。
Gap Buffer は、カーソル位置に空のメモリ領域(ギャップ)を設けることで、文字の挿入をギャップ領域に対して行うことで、編集に伴うメモリコピー不要にするもので、Emacs などで使われています。
Piece table は、元ファイルとそれに対する編集を2つのバッファで扱い、テキストの並びを Piece と呼ばれるテーブルで管理するもので、詳しくは以下を参考にしてください。
Rope データ構造とは
String → 紐、Rope → 縄 で、文字列を強化した名前が付けられたデータ構造です。
Rope では、大きなテキストを小さなチャンクに分割し、それぞれのチャンクのインデックスを二分木で管理するデータ構造です。
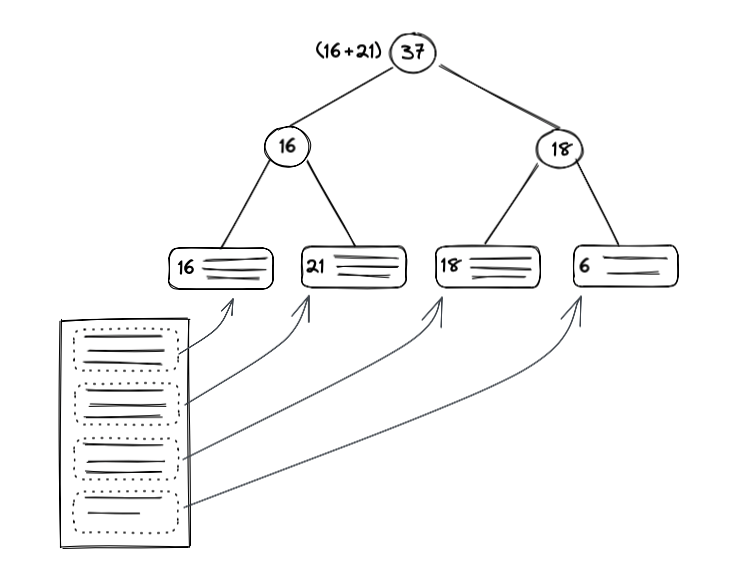
二分木のリーフノードに分割したテキストを持ち、各ノードには、左側ノードの重み(テキストの長さ)を保持します。
全体のテキストの先頭から、例えば 位置 30 の文字を得るには、以下のように二分木を辿ることで到達できます。
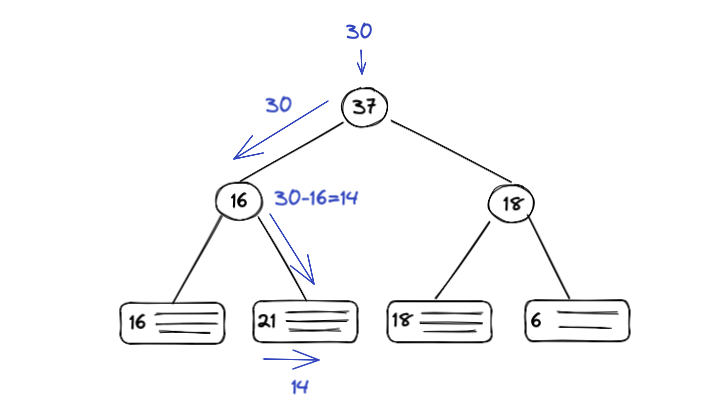
根のノードの重みは 37 で、30 の方が小さいので左子ノードに進み、重み 16 は 30 より小さいので右子ノードに進み、その際に重みからの差分である 14 検索位置として進みます。
その先はノードなので、このノードの文字列の先頭から 14 の位置が得るべき文字となります。
このように書くと分かりにくいのですが、以下のようにチャンク毎の長さをテキスト先頭からの位置を表す木構造として表現してあると考えると分かりやすいと思います。
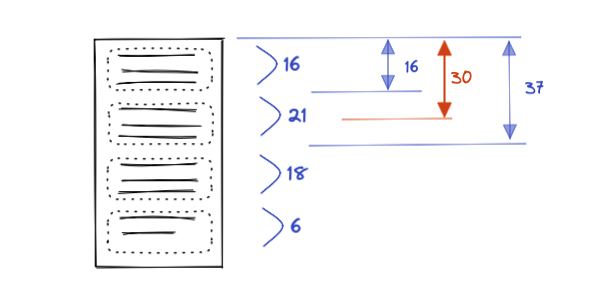
リーフ内のテキスト編集により文字長が変化した場合には、全部のノードではなく、リーフとルートノード間の経路にあるノードだけの重を変化させれば良いです。
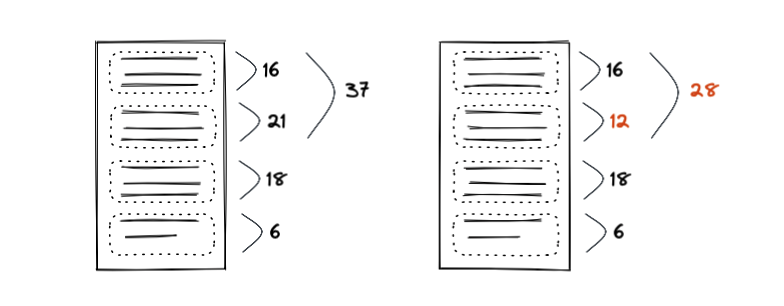
これは、先頭からの位置を木構造でインデックス化しているためです。
例えば、それぞれのチャンクがテキスト先頭からの位置をインデックスとして保持していたとすると、編集により特定のチャンクの文字列長が増えた場合、そのチャンク以降の全てのチャンクのインデックスを更新する必要がありますが、Ropeではこのようなインデックス更新が局在化されます。
リーフに格納する文字列には上限値を設け、テキストの編集に応じてリーフ・ノードの追加や削除、分割を行っていきます。また、編集の順序によって木構造のバランスが乱れるため、通常の二分木で行われるものと同様に、リバランス処理(回転)により木の長さを調整していく必要もあります。
Rope は Copy on Write の実現が容易
ここまで見てきたように Rope はテキストの保持に(特に二分木の平衡を考慮すると)それなりの複雑さを伴うデータ構造ですが、大きなメリットとして Copy on Write の実現が容易な点があります。
つまり、テキストの編集を行っても、元のテキストを保持したまま、変更後のテキストを入手できるということになります。これはテキストエディタの Undo/Redo 操作が無償で手に入るということになります(もちろんメモリは消費します)。
加えて、テキスト構造がイミュータブルとなるため、並行編集などでロックが不要になるといった利点もあります。
例えば以下のような木があり、赤い位置にリーフを挿入することを考えた場合
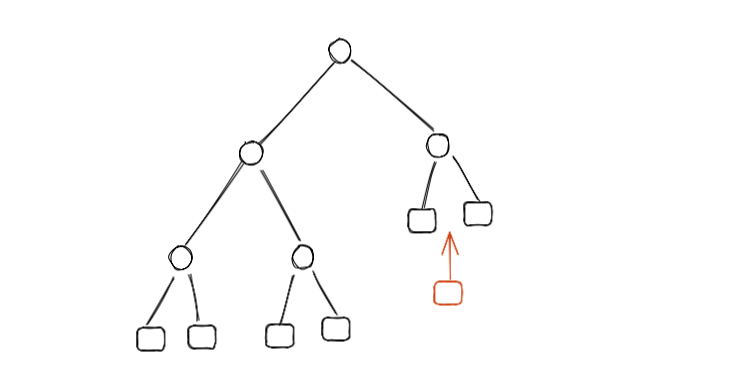
編集後の Rope は以下のようになり、左側のサブツリーは変更前と共有します。
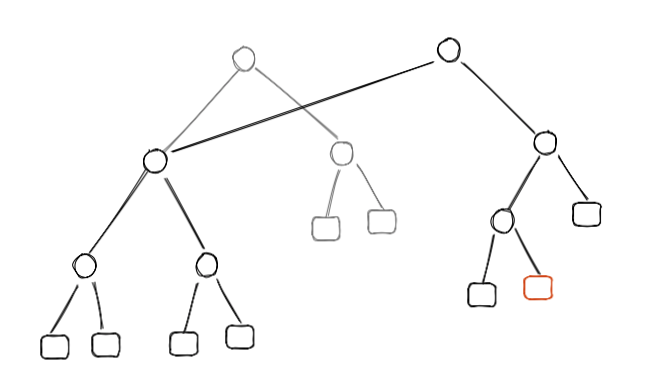
元のルートノードには編集前の構造が維持されます(図中では表現しきれていませんが、変更の無いリーフノードも共有されます)。
Rope 実装例
では、Rope の簡単な実装例を見てみましょう。
ノードは以下のように定義できます。Leaf と Branch ノードを定義します。
Leaf は(不変な)String を持ち、Branch は左右の子ノードを持ちます。
sealed interface Node { Node EMPTY = new Leaf(""); int weight(); int totalLength(); default boolean isEmpty() { return totalLength() == 0; } record Leaf(String text) implements Node { @Override public int weight() { return text.length(); } @Override public int totalLength() { return weight(); } } record Branch(Node left, Node right, int weight) implements Node { Branch(Node left, Node right) { this(left, right, left.totalLength()); } @Override public int totalLength() { return left.totalLength() + right.totalLength(); } } }
Branch は親ノードへのリンクは保持しません。親ノードへのリンク があった場合は Copy on Write を実現する際に、全てのノードのコピーが必要になるためです。
Rope は以下のようにルートノードを持ちます。
public class Rope { private static final Rope EMPTY = new Rope(""); private final Node root; private Rope(Node root) { this.root = (root == null) ? Node.EMPTY : root; } public Rope() { this.root = Node.EMPTY; } public Rope(String text) { this.root = Node.of(text); } }
Rope の結合と分割
以下のように実装できます。
public Rope concat(Rope that) { if (this.root.isEmpty()) return that; if (that.root.isEmpty()) return this; Branch newRoot = new Branch(this.root, that.root); return new Rope(balance.apply(newRoot)); }
public Rope[] split(int index) { if (index == 0) { return new Rope[] { EMPTY, this }; } if (index == root.totalLength()) { return new Rope[] { this, EMPTY }; } Node[] resultNodes = splitNode(root, index); return new Rope[] { new Rope(resultNodes[0]), new Rope(resultNodes[1]) }; }
splitNode() は以下のようになります。
private Node[] splitNode(Node node, int index) { return switch (node) { case Leaf leaf -> splitNode(leaf, index); case Branch branch -> splitNode(branch, index); }; }
ノードの分割は以下の3パターンになります。
private Node[] splitNode(Leaf leaf, int index) { String leftText = leaf.text().substring(0, index); String rightText = leaf.text().substring(index); return new Node[] { Node.of(leftText), Node.of(rightText) }; } private Node[] splitNode(Branch node, int index) { if (index < node.weight()) { // A -> A / // / \ / \ / // B node B node / -> rightPart // / \ / / \ D / \ // D E D / E leftPart G E // / \ / \ / / \ / \ / / \ // F G H I F / G H I F H I Node[] leftSplit = splitNode(node.left(), index); Node leftPart = leftSplit[0]; Node rightPart = balance.apply(new Branch(leftSplit[1], node.right())); return new Node[] { leftPart, rightPart }; } else { // A -> A // / \ / \ // B C B C / -> leftPart // / \ / \ / / \ E // D E D / E D H rightPart // / \ / \ / \ / / \ / \ \ // F G H I F G H / I F G I int rightIndex = index - node.weight(); Node[] rightSplit = splitNode(node.right(), rightIndex); Node leftPart = balance.apply(new Branch(node.left(), rightSplit[0])); Node rightPart = rightSplit[1]; return new Node[] { leftPart, rightPart }; } }
挿入と削除処理
public Rope insert(int index, String str) { if (str.isEmpty()) return this; Rope[] parts = split(index); Rope leftPart = parts[0]; Rope rightPart = parts[1]; Rope insertRope = new Rope(str); return leftPart.concat(insertRope).concat(rightPart); }
public Rope delete(int start, int end) { if (start < 0 || end > root.totalLength() || start > end) { throw new IndexOutOfBoundsException("Invalid range for deletion."); } if (start == end) return this; Rope[] parts1 = split(start); Rope leftPart = parts1[0]; Rope rightPartAndDeleted = parts1[1]; Rope[] parts2 = rightPartAndDeleted.split(end - start); Rope retainedRightPart = parts2[1]; return leftPart.concat(retainedRightPart); }
木のバランシングや細かな処理は省略していますが、おおむね以上の流れで完了です。
Rope の実行例
以下のようになります。
@Test void insertAndDelete() { Rope rope = new Rope() .insert( 0, "The quick brown ") .insert(16, "fox jumps over ") .insert(31, "the lazy dog.") .insert(10, "very "); assertEquals( "The quick very brown fox jumps over the lazy dog.", rope.toString()); Rope del = rope.delete(10, 15); assertEquals( "The quick brown fox jumps over the lazy dog.", del.toString()); // original assertEquals( "The quick very brown fox jumps over the lazy dog.", rope.toString()); }
まとめ
テキストエディタなどで使われる Rope データ構造について説明しました。
実践では、バランシングのために平衡二分木を使ったりなどさらに改善が必要ですが、実装サンプルとして以下を参照してください。
Rope はテキストをインメモリで保持する Copy on Write なデータ構造が必要な場合の良い選択肢になります。
現実的なデメリットとしては、大きなファイルを扱った際の木の初期化にコストを要する点、木構造維持のために追加のオーバーヘッドが必要な点などがあります。
メリット・デメリットは Gap Buffer、Piece table についてもそれぞれあるので、どれが一番優れているというものでは無いです。