
はじめに
本稿では Deeplearning4j を使った、ディープラーニングについて説明します。厳密な定義や数式には立ち入らず、意味合いと利用方法に焦点を当てていきます。
題材として、ディープラーニング界の Hello World である MNIST(Modified National Institute of Standards and Technology database)を使った手書き数字の画像認識を扱います。
ディープラーニングの考え方と、実際の実装をあわせて説明し、手書き数字の画像認識のアプリケーションを作成するまでをガイドします。今回は、全3回の内の 2 回目です。
損失関数
損失関数が最小の値を取るようなパラメータを見つけることが、ニューラルネットワークの学習の目的になります。しかし、パラメータ空間は広大であり、損失関数が最小値となるパラメータを有限時間内に見つけるには、何らかの戦略が必要になります。ニューラルネットワークの学習には、損失関数の勾配を利用する方法が広く使われています。
あるパラメータに着目し、そのパラメータを少し変化させた場合に、損失関数がどのように変化するかという変化量、つまり「傾き」をパラメータの更新量に反映させるという手法が勾配法です。この様子を例としてグラフにしたものを見てみましょう。横軸がパラメータの値、縦軸が損失関数の結果とします。

①の時点では、グラフの傾きが大きいため、損失関数の最小値から離れていると言えます。②の時点では、傾きが小さくなってきたため、損失関数の最小値に近づいていると考えられます。③の時点では、傾きが 0 となっているため、損失関数の(局所的な)最小値に達していると考えることができます。
ただし、このグラフにおける最小値はさらに右側にあり、③ の位置は局所的な最小値となっています。誤った局所解に達しているとは言え、傾きをヒントにパラメータを更新することで、闇雲にパラメータを探索するのではなく、効果的に最小値を見つけることができ、これが損失関数の傾きを使った勾配法の基本的な考え方になります。
グラフの傾きは、損失関数を微分することにより求められるため、得られた微分に対して、パラメータをどの程度更新するかという係数を掛けたものをパラメータの更新量として利用します。傾きが大きければ損失関数の極値からは離れているため、その傾きの大きさを係数にして大きくパラメータを更新する。逆に傾きが小さければ、その付近に存在するであろう損失関数の極値を細かく探すという戦略です。このようにすることで、傾きが大きな最小値から離れた場所では更新量が大きくなり、早く極値に到達するようになります。更新の係数は学習量(learning rate)と呼ばれ、学習の前に何らかの方法で値を決定する必要があります。この値は、大きすぎても小さすぎても学習を効率良く行うことができなくなるため、学習の結果を確認しながら学習率を調整していくことになります。
ここで、Deeplearning4j での学習率の指定を見ておきましょう。学習率の指定は updater() にて指定しています。
MultiLayerConfiguration conf = new NeuralNetConfiguration.Builder() .seed(123) .updater(new Nesterovs(0.006, 0.9)) .l2(1e-4) // ...
Nesterovs は 学習率に Momentum法 を用いるものとなります。第一引数には学習率、第二引数には慣性量を指定しています。これは、前回の更新量を覚えておき、同じ方向へのパラメータ更新が続く場合は、その方向への更新が加速され、前回と逆の方向へのパラメータ更新が行われた場合には、更新を減速(学習率を小さく)することで、パラメータの収束を効率化するものです。お椀のふちからパチンコ玉を転がすことを想像するとイメージしやすいでしょう。
損失関数の勾配と誤差伝搬法
損失関数の傾きを利用して、パラメータの更新量を調整することは分かりましたが、この傾きはどのように求めれば良いでしょうか。
ある関数が以下のようなグラフとなった場合、x 点における傾きは、x に微小なdを加えた点を通る直線の傾きを考えることで近似できます。このdを無限にゼロに近づけることで、x点における傾きを得ることができます。
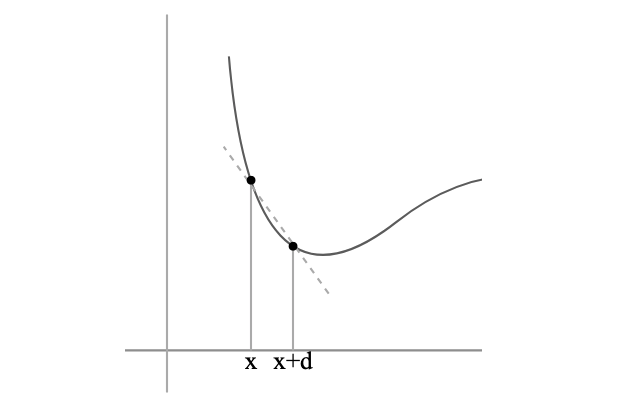
d の値を可能な限り小さく取り、x点における真の傾きとの誤差が十分小さければ、それは x 点における微分ということができます。このようにして求めた微分を数値微分と呼び、ある点における微分値を、コンピュータによる計算にて得ることができます。
ここでのグラフは、2次元座標上のグラフであり簡単なものですが、ニューラルネットワークでは、膨大な数のパラメータが存在するため、次元数が非常に大きくなります。多数のパラメータに対する傾きは、偏微分により得ることを考えます。偏微分と言うと難しそうに感じますが、あるパラメータを1つだけ変化させ、その変化に応じて結果がどの程度変化するかを考えるだけです。つまり選択したパラメータ以外は固定化された定数として扱い、選択したパラメータがどの程度結果に影響を及ぼすのかを考えるということになります。このようにして得た各パラメータにおける偏微分をまとめたものをベクトルとして考えたものを勾配と呼びます。このベクトルの指し示す方向が、関数の値を最も減らす方向となります。
それぞれのパラメータを、1つずつ、微量だけ変化させ、損失関数の変化量を求め、パラメータの更新は、その変化量に応じて各パラメータを変化させる。これがパラメータ更新の1つの戦略となります。しかしこのような方法では、数値微分の計算における誤差の影響や、多数のパラメータ毎に行う計算量の問題などもあり、効率的な方法とは言えません。そこで考えるのが、数学的な微分となります。数学的に微分をとることで、ある点における傾きは数学的に導出できるようになります。多数のパラメータが存在するニューラルネットワークに関しては、誤差逆伝播法(Backpropagation) を使うことでパラメータに関する損失関数の勾配を効率よく計算することができます。誤差伝搬法について詳細は述べませんが、ニューラルネットワークの各ノードの出力値を記録しておき、出力層の微分結果から、ノードを逆方向にたどっていくことで、各パラメータに関する微分を芋づる式に(連鎖律という定理を使い)得る方法です。
Deeplearning4j では、ニューラルネットワークのビルダにて以下のように指定することができます。BackpropType.Standard の他に BackpropType.TruncatedBPTT を指定することができますが、デフォルト値としてBackpropType.Standardが使われるため、通常は指定することは少ないでしょう。
MultiLayerConfiguration conf = new NeuralNetConfiguration.Builder() // ... .backpropType(BackpropType.Standard) .build();
勾配消失
ここまでで、ニューラルネットワークにおける学習(重みパラメータの更新)は、損失関数の勾配を使うことで効率良く達成できることを見てきました。パラメータの更新では、損失関数の勾配に学習率(任意に定めた定数)を乗じた値を更新量として、次の学習時のパラメータ値を決定します。
あるパラメータの現在の値を w1 とした場合、更新後のパラメータは(η を学習率として定めた任意の定数、u を損失関数の勾配とした場合)、 w2 = w1 - ηu のように表すことができます(引き算となっているのは、傾きの逆方向に移動するためです)(その他様々な更新アルゴリズムが存在します)。
損失関数の勾配(式中のu)がゼロまたはゼロに非常に近くなった場合に何が起こるでしょうか。パラメータの更新量が極端に小さくなるため、パラメータの値がほとんど変化しなくなります。パラメータの値が更新されなければ、学習が進まなくなり、最悪の場合には学習が停止してしまうことになります。このような状況は勾配消失(gradient vanishing)と呼ばれ、特に層の深いネットワークの学習を阻害する原因となります。
活性関数としてシグモイド関数を使ったケースを考えてみます。

シグモイド関数は、入力にどのような値があったとしても、出力は0〜1の範囲に収まります。そして傾きは、入力がゼロの場合に最も大きくなり、その値は(標準シグモイド関数の場合)0.25となります。これは、シグモイド関数は入力信号を減衰させる関数として働くことを意味します。入力信号が非常に大きな値であったとしても、出力信号は1未満の値に減衰されます。また、シグモイド関数のバイアスを無視した場合(上記グラフの原点座標をy軸の 0.5 に移動させた場合)、出力値は、大きくとも入力値が0.25倍された値にしかなりません。
減衰方向に働く活性関数(傾きが0〜1の範囲)を用いたネットワークでは、入力層に近い側のパラメータは、出力結果である損失関数の値に影響を与えにくいことは直感的に理解できると思います。最終的な出力となる損失関数の値に影響度を発揮するのは、出力層に近い層のパラメータであり、入力層に近い側のパラメータの変化は、層を重ねる毎に影響を弱めることになります。損失関数に影響を与えにくいということは、勾配がゼロに近いことを意味するため、学習を進めても入力に近い層ではほとんどパラメータが更新されない結果となります。入力に近い層が非常にゆっくりと学習を進める間に、出力側の層の学習だけが進むため、入力に近い層での勾配はゼロに近づきます。入力に近い層では活性関数の値に影響を与えないため、これらの層はあっても無くても変わらないということになります。
このような問題があるため、現在ではシグモイド関数に変え、傾きの最大値が1となるtanh関数や、先に述べた ReLU(Rectified Linear Unit)などの勾配消失を起こしにくい関数を活性関数として選択するようになっています。
重みの初期値
勾配消失によりニューラルネットワークの学習が進まなくなることを見てきましたが、パラメータ(重み)の初期値も効果的に学習を行うための重要なポイントとなります。
例えば先ほどのシグモイド関数では、入力がゼロから離れた値となるにつれ、出力値はほとんど動かないといった状況になります。入力値に対して最も敏感に反応するのは入力値がゼロのケースであり、入力値をゼロに近い値に適度にまとめることが学習を進める上で効果的になります。ReLUに関しても、ゼロを境として出力の挙動を変える関数となっています。このように、活性関数は、ゼロ付近でその特徴を強く発揮する関数になります。学習を効率的に行うには、活性関数への入力がゼロ付近にまとまった形とすることが有効であり、パラメータの初期値はゼロに近い値とする必要があります。そしてこの初期値は、適度にバラけた値である必要もあります。ネットワーク全体で均一な初期値を与えてしまうと、学習の過程で、(ニューロン同士は全結合しているため)各パラメータが同じように更新されてしまい、パラメータの数を増やす意味が薄れてしまうためです。
パラメータの初期値をどのように決定するかは、多くの場合、正規分布の考え方を基本とします。正規分布は、ゼロ付近の値が発生しやすく、ゼロから離れた値は発生しにくいという釣鐘型の分布を示すものとなります。標準偏差を小さくすることにより、よりゼロ付近に値が集中することになるため、学習効率の良い標準偏差を見つけて、これにより初期値を決定する方法が取られます。しかし、適切な値については決定的なものは存在せず、利用する活性関数や解決すべき問題に応じて適切なものを見つける必要があります。
先の例では以下のようにネットワーク層の定義を以下のように行いました。
new DenseLayer.Builder()
.nIn(HEIGHT * WIDTH)
.nOut(1000)
.activation(Activation.RELU)
.weightInit(WeightInit.XAVIER)
.build()
この層では、.weightInit(WeightInit.XAVIER)としてこの層のパラメータの初期値を与えています。これは「Xavier の初期値」という方法で初期値を与えることを指示するもので、前層のノードの数を n とした場合、√(1/n) の標準偏差を持つ分布を使います。前層のノードが多い場合には、初期値がよりゼロに近い値に集中することになります。各層毎の初期値の分布を均一におしなべた分布とすることで、効率的な学習を可能とするものです。なお、活性関数として ReLU を使う場合には、√(2/n) の標準偏差にて、より広がりのある初期値を与えることが良いとされています。これは「Heの初期値」と呼ばれるものです。
過学習と正規化
ニューラルネットワークのモデルが、学習用のデータセットに過度に適合した状態を過学習(overfitting)と言います。手書き数字の画像認識の例で考えると、数字画像の特徴量に加え、ノイズ値や外れ値など、本質的な特徴量以外を学習してモデルに反映しまっている状況です。未知の画像データに対して分類を行うためには、個々の画像としてではなく、抽象度の高い、数字としての特徴量を学習する必要があるのです。
過学習は、大量のパラメータを持つ表現力の高いモデルを使った場合や、訓練データが少ない場合に顕著に現れてきます。この過学習を抑制するには、パラメータの値をネットワーク全体として小さくなるような制限を設けることで、特定の入力に過度に反応しない、なめらかなパラメータ配分を目指すことが有効になります。損失関数に対してパラメータの和を加え、これらを同時に最小化するようなペナルティを課すという手法です。この手法には L1正規化 や L2正規化 と呼ばれるものがあります。
Deeplearning4j によるネットワーク層の定義は以下のように行うことができます。
MultiLayerConfiguration conf = new NeuralNetConfiguration.Builder() .seed(123) .updater(new Nesterovs(0.006, 0.9)) .l2(1e-4) .list()
この定義において、.l2(1e-4) の部分により L2正規化 を指示しています。
L2正規化では正則化項をL2ノルムで定義します。L2ノルムとは各要素の二乗和の平方根をとったもので、いわゆる一般的な意味での 距離 を表します。つまり全てのパラメータの大きさを、パラメータのベクトルとして考え、そのベクトルの長さが大きくならないような制限を設けることになります。
パラメータ数が2つの場合で考えれば、その距離は、以下のように考えることができます。

ピタゴラスの定理、または三平方の定理による、直角三角形の斜辺の計算と同じです。ここではパラメータが2つの2次元となっていますが、パラメータの数がN個となっても同じく、二乗和の平方根により距離としての値を得ることができます。
学習には、L2ノルムと損失関数の値の合計が小さくなるように各パラメータを更新していきます。(なお、L1正則化では、パラメータの絶対値の和を使います)。 .l2(1e-4) の引数は、L2ノルムに乗じる定数で、L2正規化の影響をどの程度考慮するかという倍率となります。
手書き数字の画像認識の実装
ここまでで、手書き数字の画像認識を行うための基本となる事柄を整理してきました。
次回はこの内容を踏まえて、Deeplearning4j による実装を進めていきましょう。

